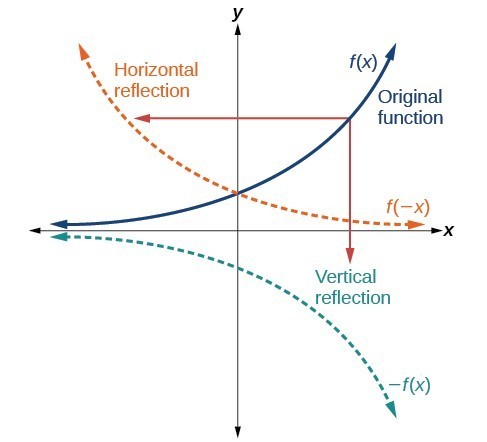
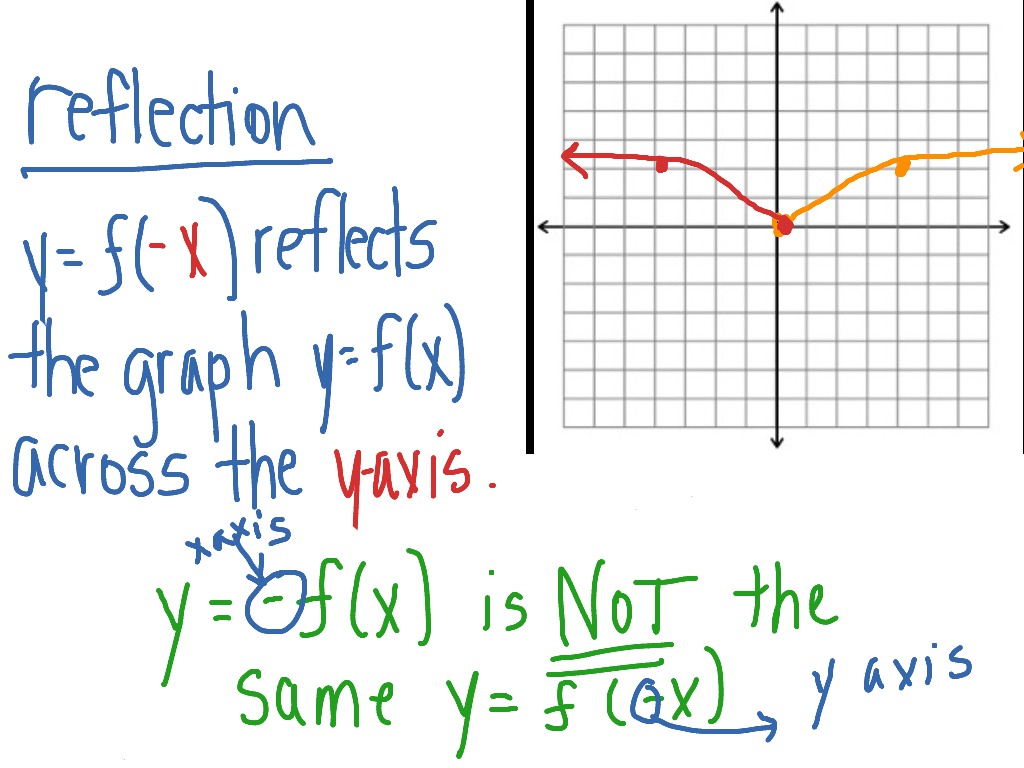
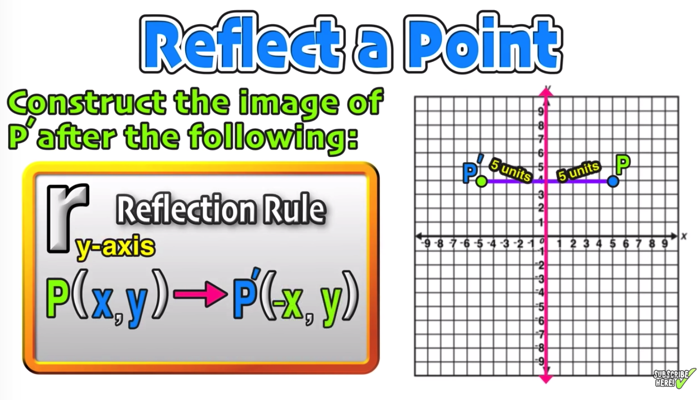
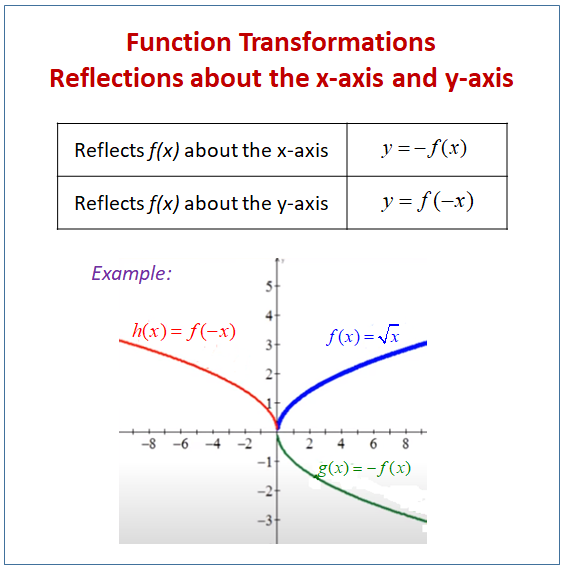
In that light being originates from the second quadrant with the equation X plus y equals one We could go ahead and rearrange that and solve for why?The relection of the graph of f( x,y) = 0 in the xaxis is f(x, —y) = 0 So the image of the line y=2x in the xaxis is —y = 2x or y = —2xF ( x) \displaystyle f\left (x\right) f (x), a new function g ( x) = f ( − x) \displaystyle g\left (x\right)=f\left (x\right) g(x) = f (−x) is a horizontal reflection of the function f ( x) \displaystyle f\left (x\right) f (x), sometimes called a reflection about the y axis
Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line
Reflection over x axis vs y axis equation
Reflection over x axis vs y axis equation-The reflection of such a parabola over the xaxis is simply written as y = (x^2) In other words, the function of f ( x ) becomes f ( x ) when reflected over the x axisThe rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
The equation of the line of symmetry To describe a reflection on a grid, the equation of the mirror line is needed Example Reflect the shape in the line \(x = 1\) The line \(x = 1\) is aStack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe answer from question (1) is reflected in the line x = 4 What is the equation of the image?
Reflection of the square root function over the yaxis Square Root Function Reflection of the Square Root Function across the yaxis Now, I know the domain of a square root has to be equal to or greater than zero So that's when imaginary numbers are used Right?Identifying coordinates of figures' reflections In this lesson students examine the impact on coordinates when a figure is reflected over the xaxis and yaxis They also learn to apply algebraic representations and analyze graphed images Students learn that a reflection is a mirror image of a figure over the line of reflectionIs the graph of y=x²
Odd Function A function f f is called an odd function if f(x)= −f(−x) f ( x) = − f ( − x) for all x x in the domain of f f In other words, a function is odd if performing a reflection about the y y axis and x x axis (doesn't matter which is performed first) does not change the graph of the function To help remember the definitionWhen you reflect a point across the yaxis, the ycoordinate remains the same, but the xcoordinate is transformed into its opposite When working with the graph of y = f (x), replace x with x Reflection in y = x When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change placesReflect Over XAxis Definition Reflection over the xaxis is the process of producing a coordinate point that is mirrored across the xaxis of the coordinate plane That is it has the same X coordinate and opposite y4 coordinate



Transforming Exponential Functions



Reflect Function About Y Axis F X Expii
Write the equation for the final transformed graph of f after the indicated transformations are applied to its graph f(x) = 4\sqrt{x}, reflect in the yaxis and shift upwards 5 unitsThereof, how do you reflect a log over the y axis?The graph of y=k⋅x²



Operations On Functions Reflections And Rotations Sparknotes



Reflection Rules How To W 25 Step By Step Examples
Y axis) Reflection over line y=x or y=Reflection over line y=x or y=xx Reflection over y=x Point (x,y) reflects to point (y,x) Reflection over line y=xAn image created by a reflection will always be congruent to its preimageThis video shows reflection over the xaxis, yaxis, x = −3, y = 5, y = x, and y = − x Show Video Lesson Reflections using Matrices This lesson involves reflections in the coordinate plane We use coordinate rules as well as matrix multiplication to reflect a polygon (or polygon matrix) about the xaxis, yaxis, the line y = x or the



Scaling Reflecting Parabolas Video Khan Academy




Question Video Writing The Equation For A Square Root Function Obtained By A Reflection In The 𝑦 Axis Nagwa
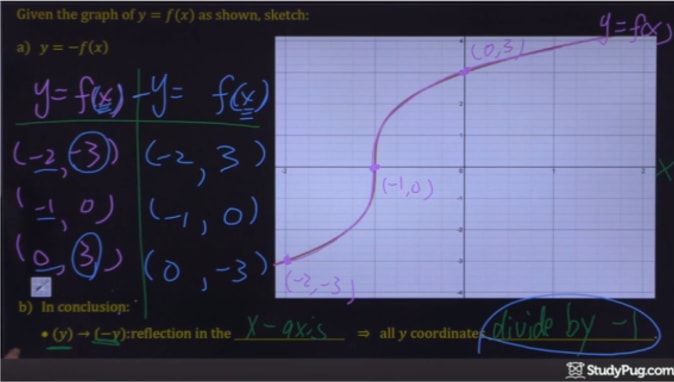
Step 1 Know that we're reflecting across the xaxis Since we were asked to plot the – f (x) f(x) f (x) reflection, is it very important that you recognize this means we are being asked to plot the reflection over the xaxis When drawing reflections across the x x x and y y y axis, it is very easy to get confused by some of the notationsIt makes sense but at he same time it doesn't because when I pump the reflectedOn this lesson, you will learn how to perform reflections over the xaxis and reflections over the yaxis (also known as across the xaxis and across the ya



Reflection Across The Y Axis Math Functions Showme



1 5 Shifting Reflecting And Stretching Graphs
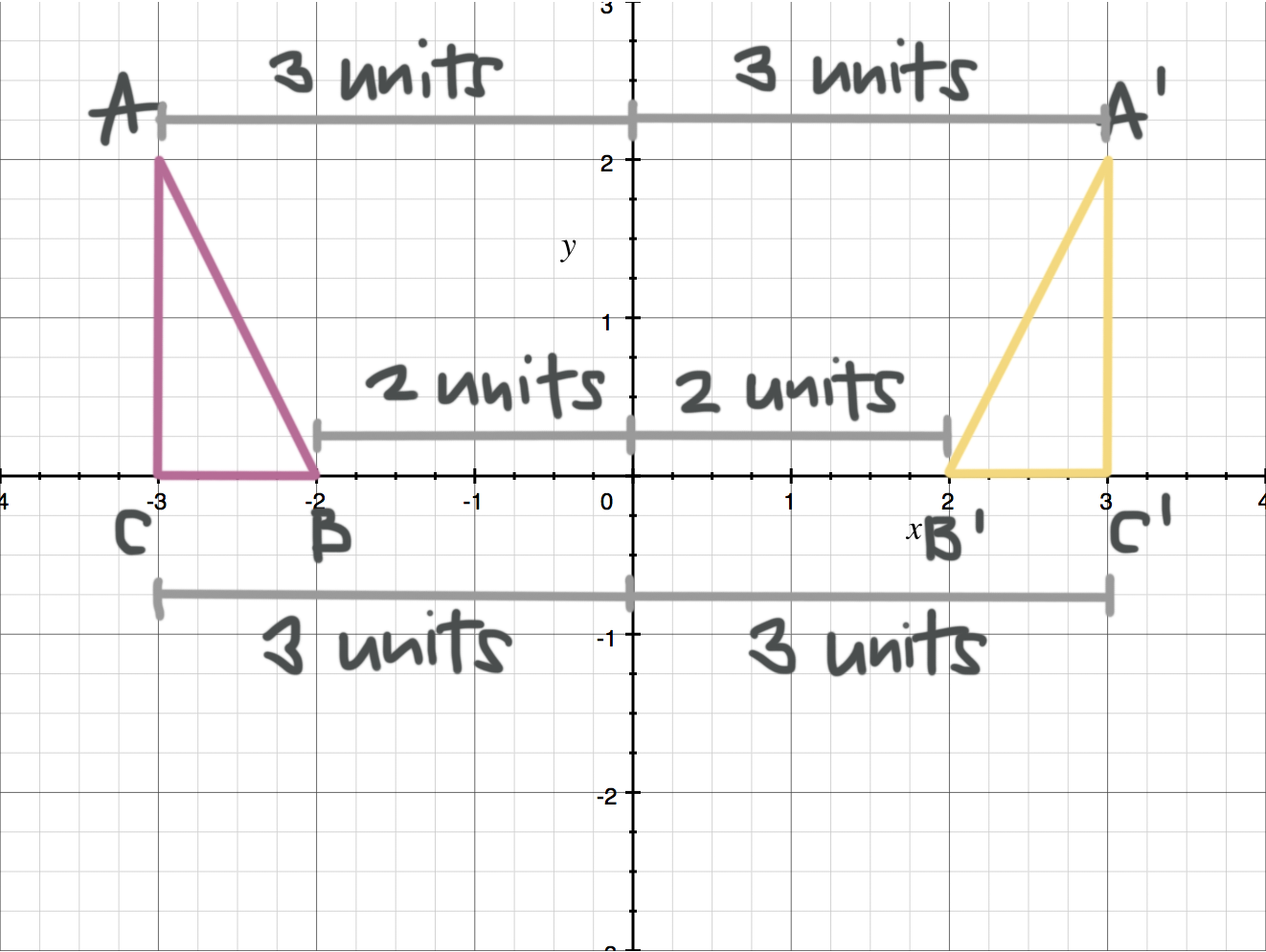
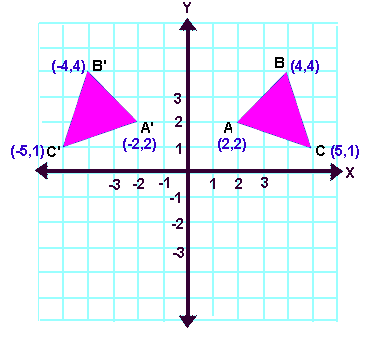
Apply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflectionFunctions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and imagesExample 3 Triangle PQR has the vertices P(2, 5), Q(6, 2) and R(2, 2) Find the vertices of triangle P'Q'R' after a reflection across the xaxis Then graph the triangle and its image Solution Step 1 Apply the rule to find the vertices of the image




Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
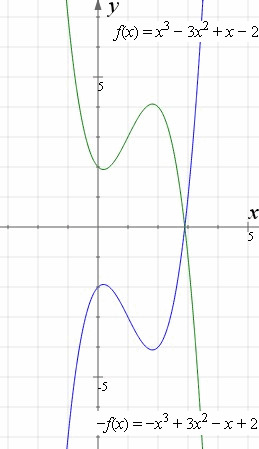
Rewrite the equation by factoring out a 1 from the exponent to read From the equation, you can see that the horizontal shift will be to the left 10 units and there will be a reflection over the yaxisTherefore, reflect the graph of over the yaxis and then shift (move) the reflected graph left 10 unitsFig 3 is the reflection of Fig 1 about the yaxis Every point that was to the right of the origin gets reflected to the left And every point that was on the left gets reflected to the right In other words—every x becomes −x Only the yintercept is invariant The equation of the reflection of f(x) about the yaxis is y = f(−x)The line y = 15x – 2 is reflected in the line y = 1 What is the equation of the image?



Horizontal



Parabola Scalings And Translations Zona Land Education
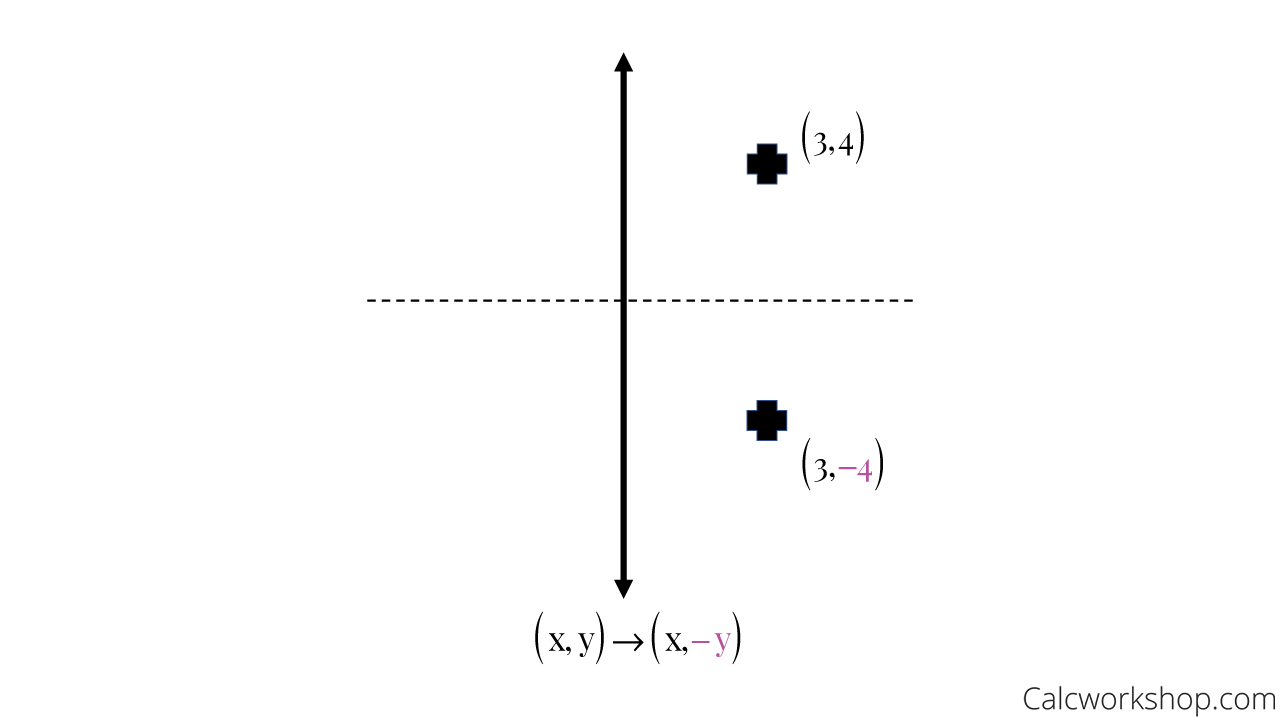
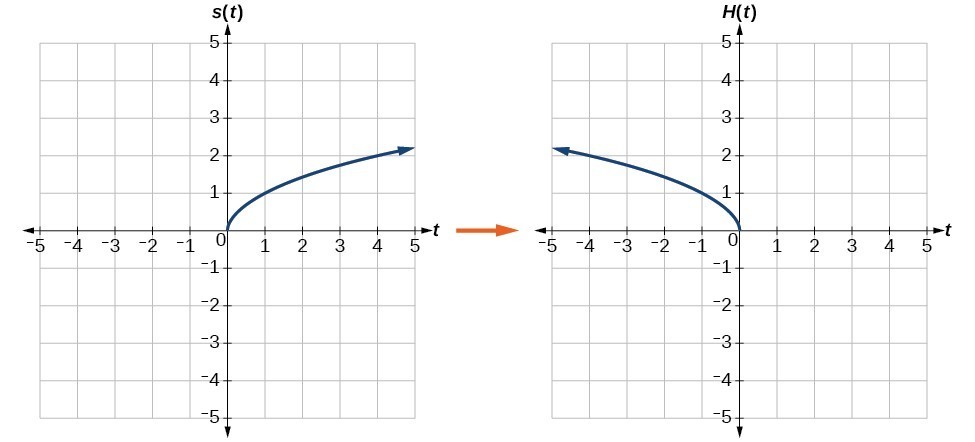
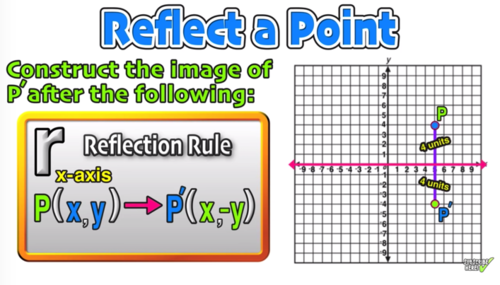
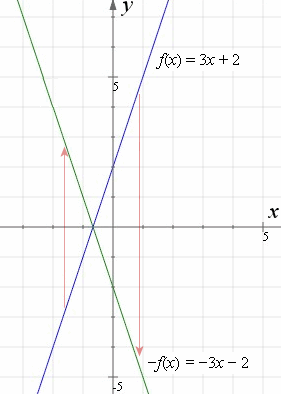
A reflection of a point over the x axis is shown The rule for a reflection over the x axis is ( x, y) → ( x, − y)This video explains to graph graph reflections across the xaxis and yaxis in the form a*f(b(xc))d This video looks at how the sign of a and b affect thGraphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the x axis or the y axis When we multiply the parent function f (x) = bx f ( x) = b x by –1, we get a reflection about the x axis When we multiply the input by –1, we get a reflection about the y axis




Pre Cal 40s Fall 06 Scribe Transformation




Cartesian Coordinate System Wikipedia
A math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression Let's talk about reflections Now recall how to reflect the graph y=f of x across the x axisWhen reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection over the line y=x By following the notation, we would swap the xvalue and the yvalueAnd also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxis



Assignment 2 Transforming Parabolas



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line
We can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems Google Classroom Facebook Twitter EmailReflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Geometry reflection A reflection is a flip of an object over a line Let's look at two very common reflections a horizontal reflection and a vertical reflection



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaReflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaEvery point below the xaxis is reflected to its corresponding position above the xaxis Contents Reflection over the xaxis for Sets of Coordinates (x, y),



Ch 3 4



Reflection
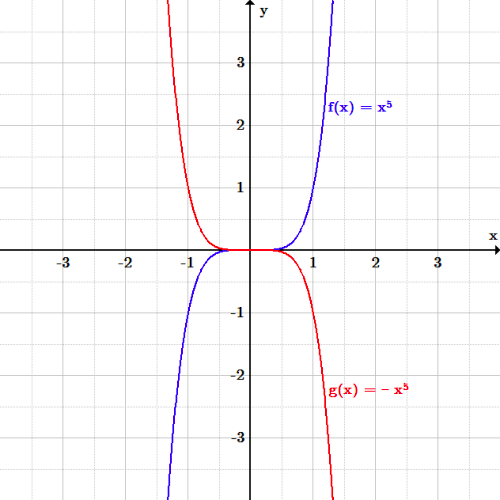
I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0 If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^xThe rule for a reflection over the x axis is (x,y)→(x,−y) What is true reflection?Reflection over the xaxis is a type of linear transformation that flips a shape or graph over the xaxis Every point above the xaxis is reflected to its corresponding position below the xaxis;




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
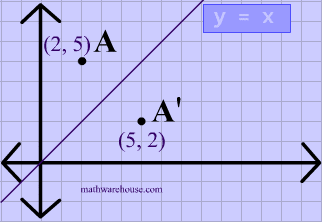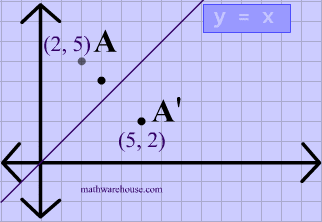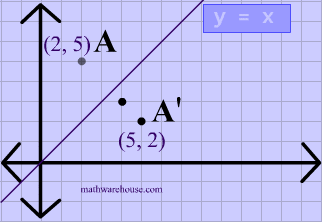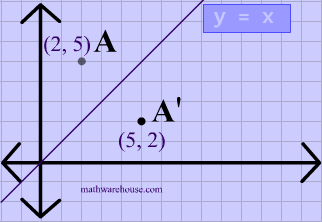
Remember that when a point P (x, y) of the coordinate plane is reflected in the y axis , it becomes the point Q (x, y) and when reflected in x axis, it becomes P' (x, y) Therefore the quadratic p (x) = ax^2 bx c (a not zero) when reflected in y axis it becomes ;Reflection A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a line of symmetry using a reflection matrixReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (B, A ) $



Assignment 2 Transforming Parabolas



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = a√x− hk y = a x h k Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 y = √x y = x Find a a, h h, and k k for y = √x y = x a = 1 a = 1So that would end up giving us why Subtract the X over equals negative X plus one And we're going to go ahead and plot this up until the X axis And so it's going to start up at positive oneScaled by a factor of k If k<0, it's also reflected (or flipped) across the xaxis In this worked example, we find the equation of a parabola from its graph Transforming quadratic functions Intro to parabola transformations
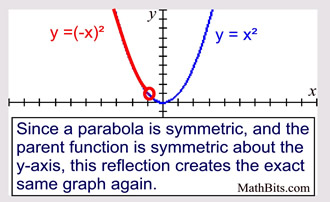



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
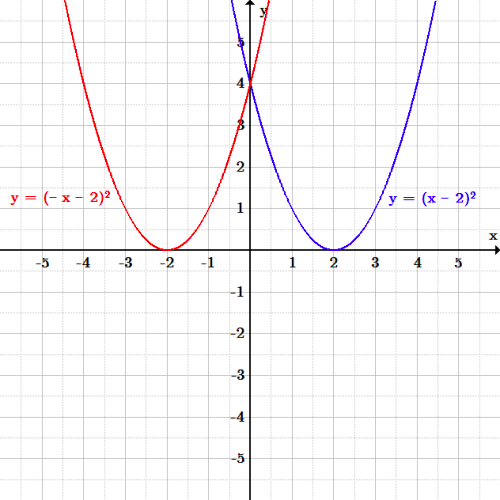



Transformations Boundless Algebra
Reflection over x axis equation Since the reflection applied is going to be over the xaxis that means negating the yvalue For example if we begin by graphing the parent function latexfleftxright2xlatex we can then graph the two reflections We are not concerned about other transformations that take F x displaystyle fleft xright f x a new functionReflection across the yaxis y = f ( − x) y = f (x) y = f ( − x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versa Basic Concepts
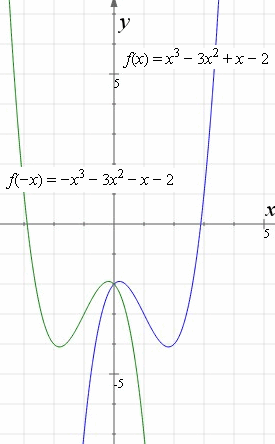



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



Coordinate Plane
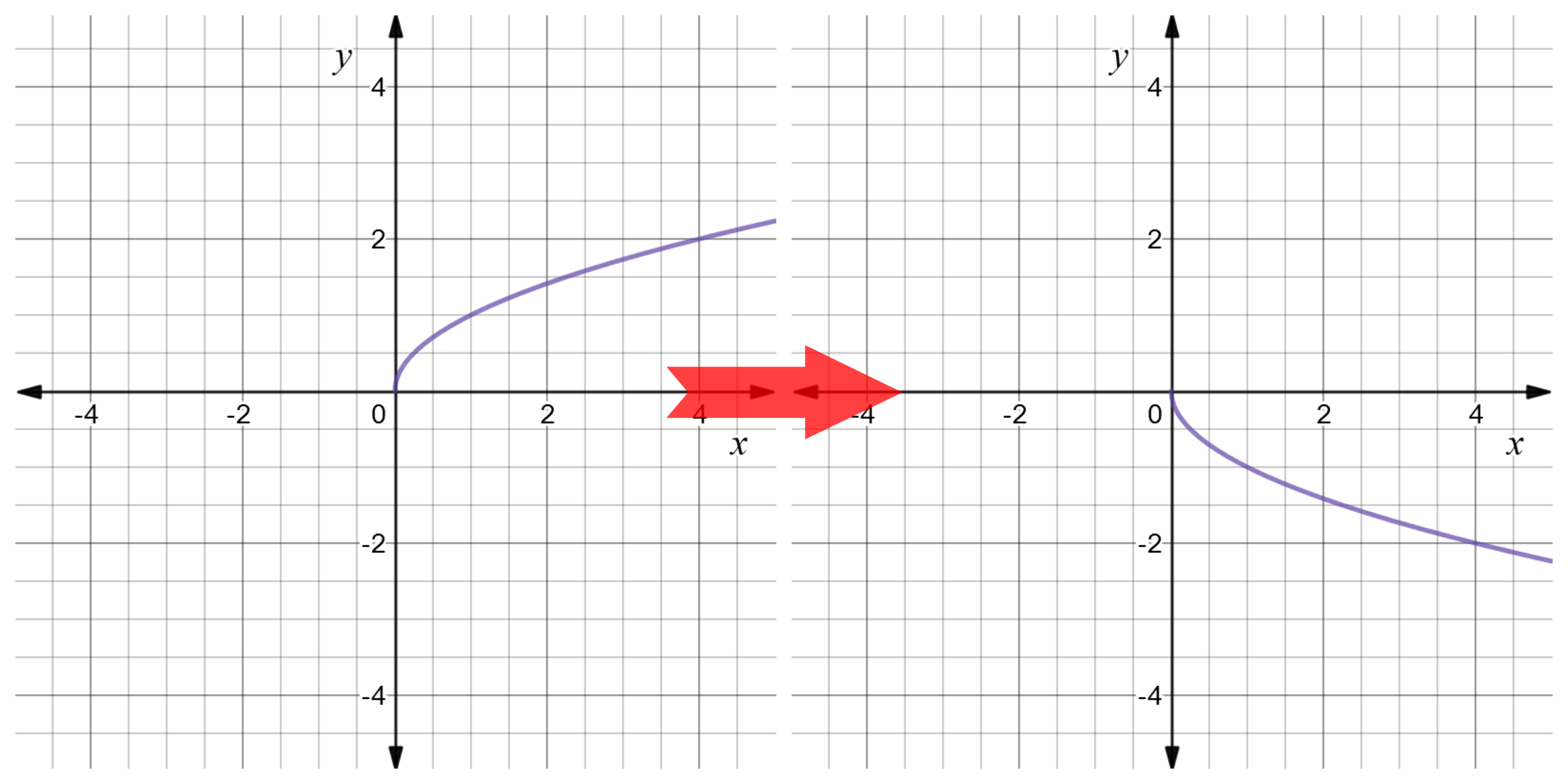



Reflect Function About Y Axis F X Expii
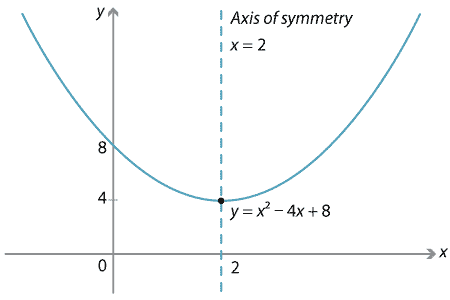



Content Transformations Of The Parabola




The Transformation Of The Graph Of A Quadratic Equation Matherudition
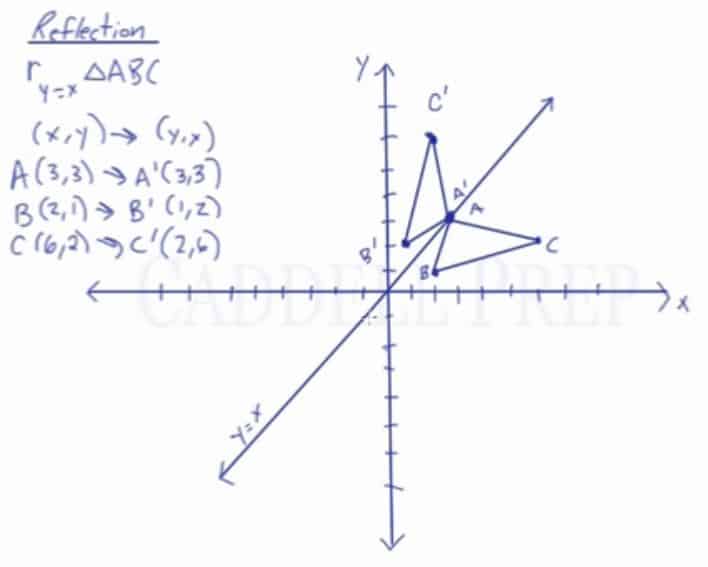



Learn About Reflection Over The Line Y X Caddell Prep Online



A Review Of Logarithms
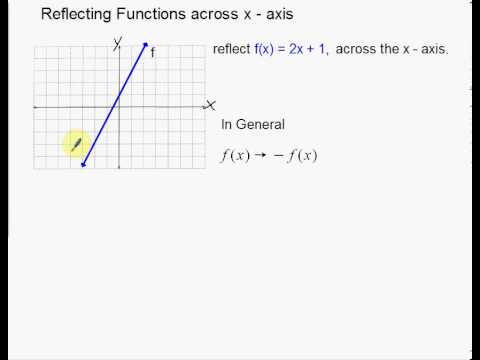



Linear Reflections Across X And Y Axis Youtube
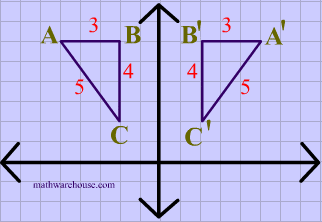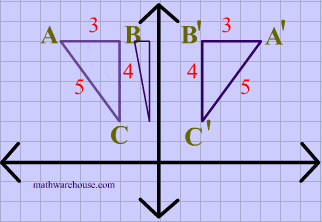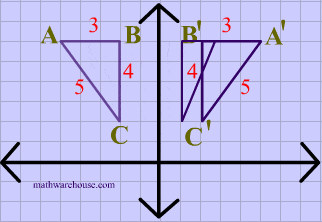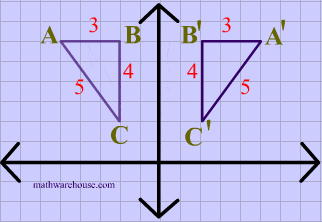



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
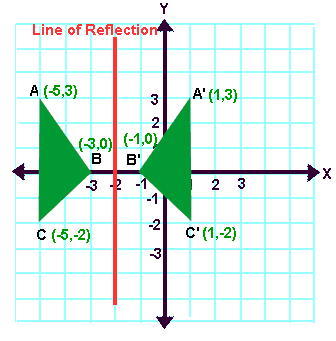



Unit 6 Topic 2 Other Line Reflections Williamsburg High School For Architecture And Design
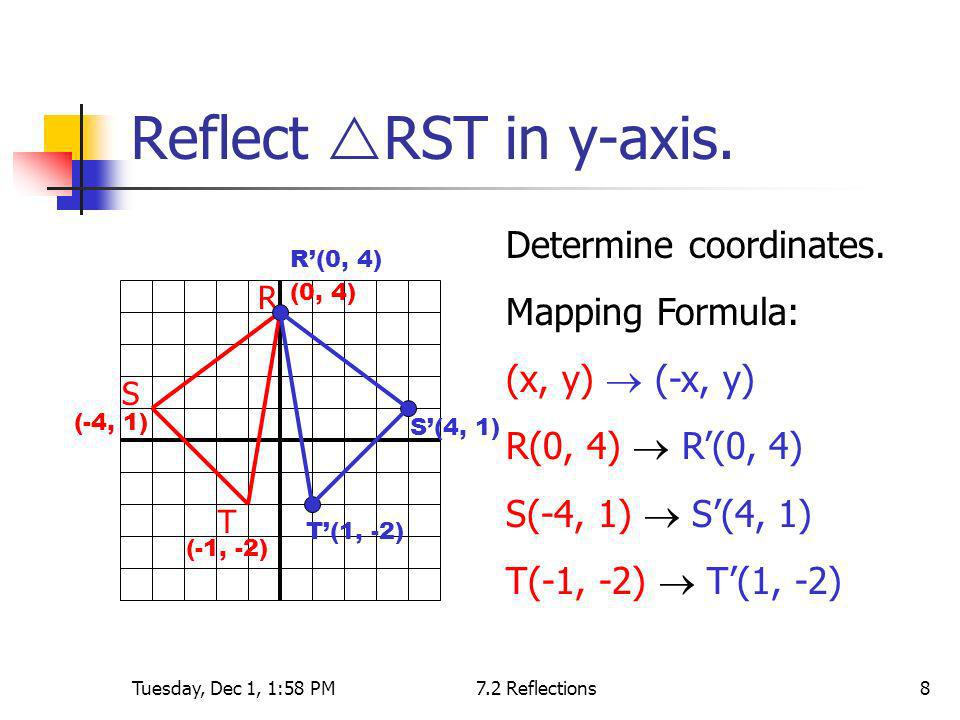



What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic
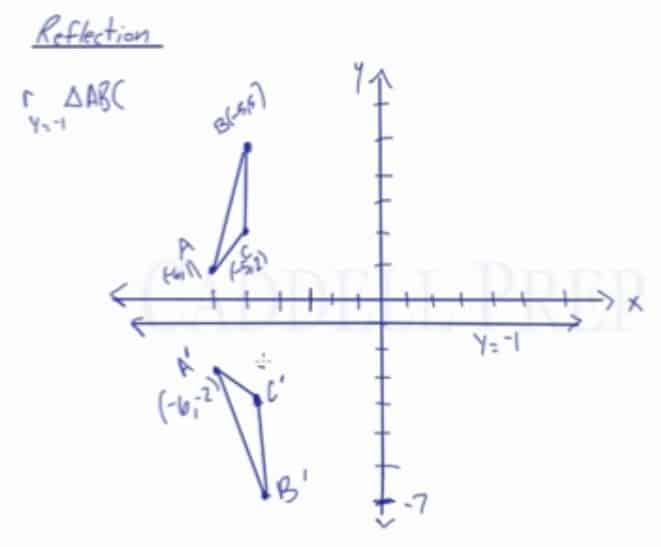



Learn About Reflection Over A Horizontal Or Vertical Line
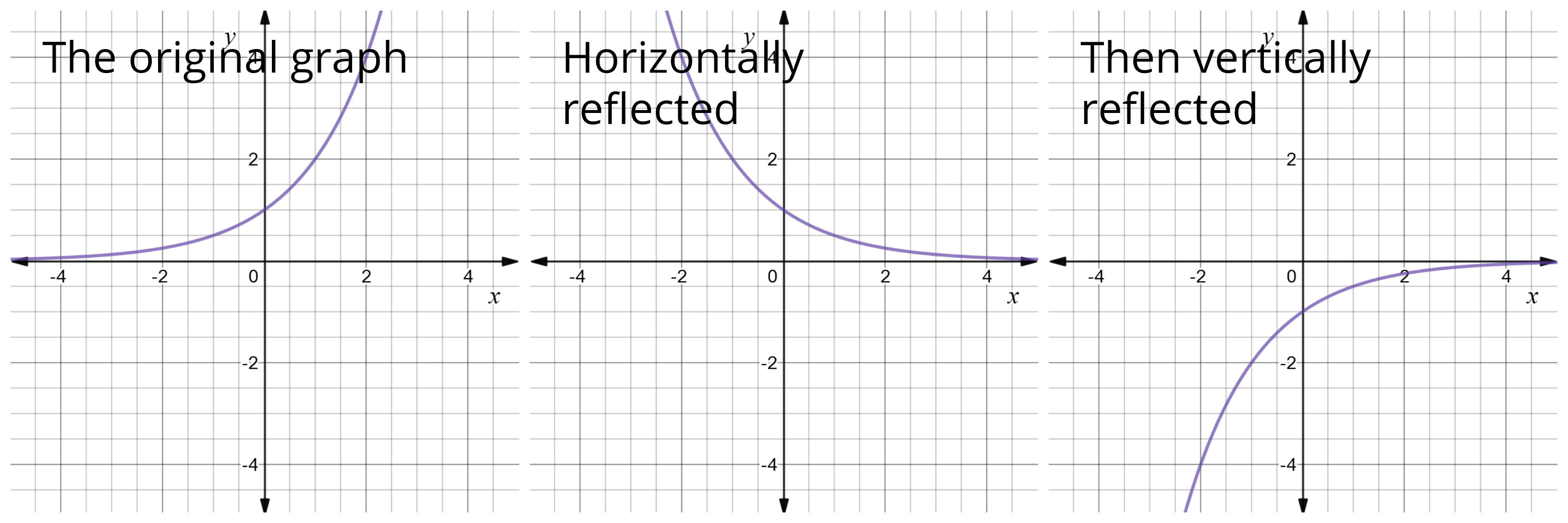



Reflect Function About Y Axis F X Expii



Transformation Reflection Over X Axis
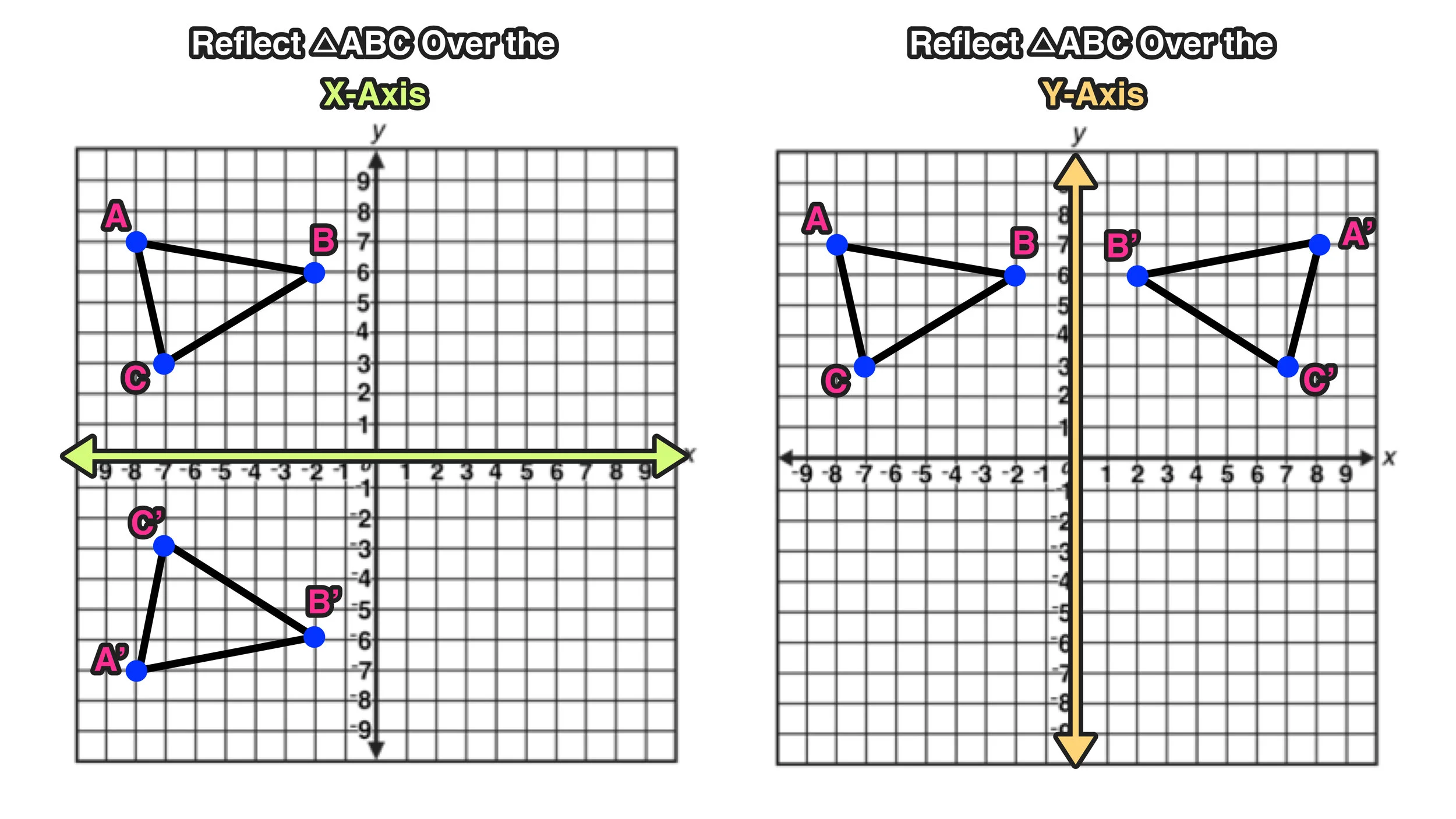



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Reflection Over The X And Y Axis The Complete Guide Mashup Math
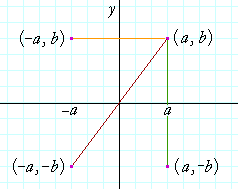



Reflections Of A Graph Topics In Precalculus
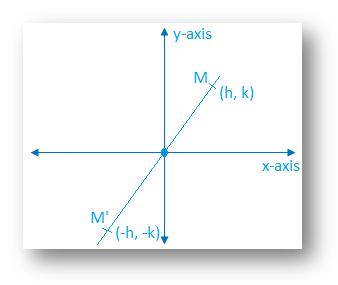



Reflection Of A Point In Origin Reflected In The Origin Worked Out Examples
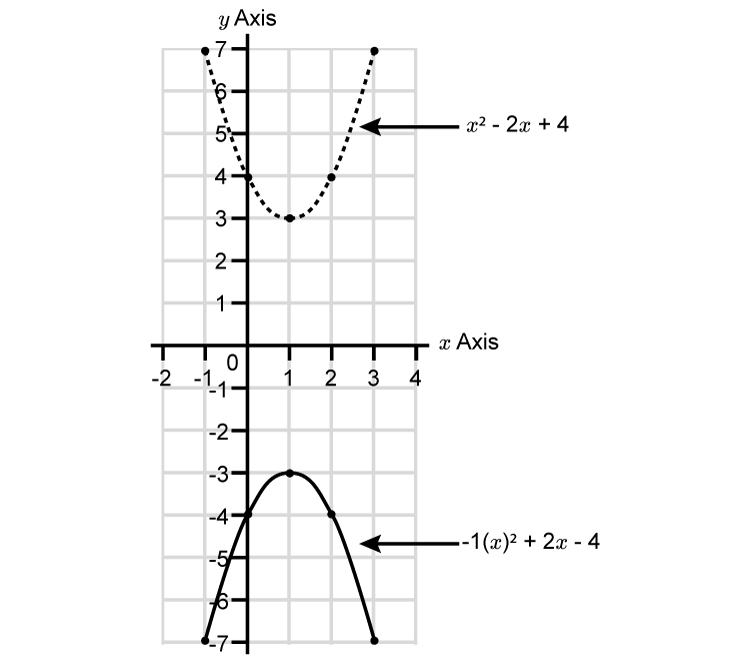



Reflecting More Difficult Parabolas Mammoth Memory Maths



Reflection Transformation Matrix




Want Brainliest Get This Correct What Is The Equation Of This Function After It Is Reflected Over Brainly Com



Operations On Functions Reflections And Rotations Sparknotes




Polar Graph Polar Equation Symmetry Reflection X Axis Symmetric About The X Axis Homework Help Videos Brightstorm



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities



How To Horizontally Transform A Function Dummies



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




Reflection Across The X Axis Reflection Math Chart
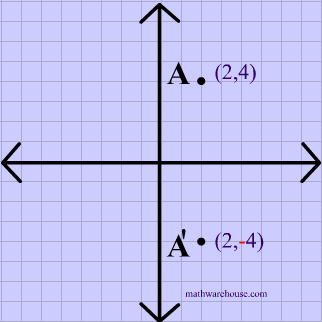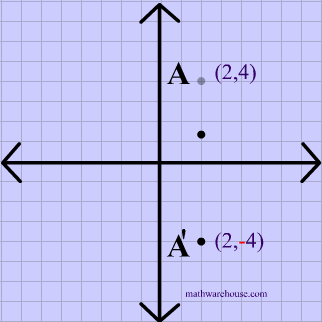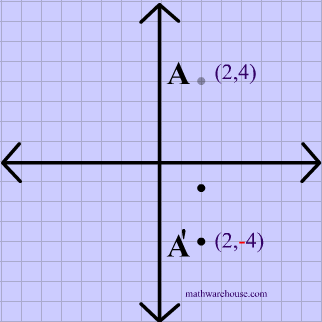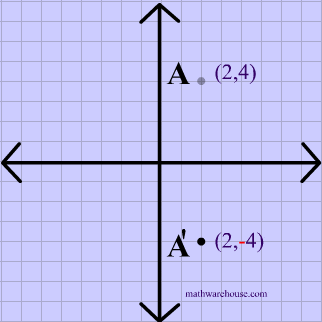



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
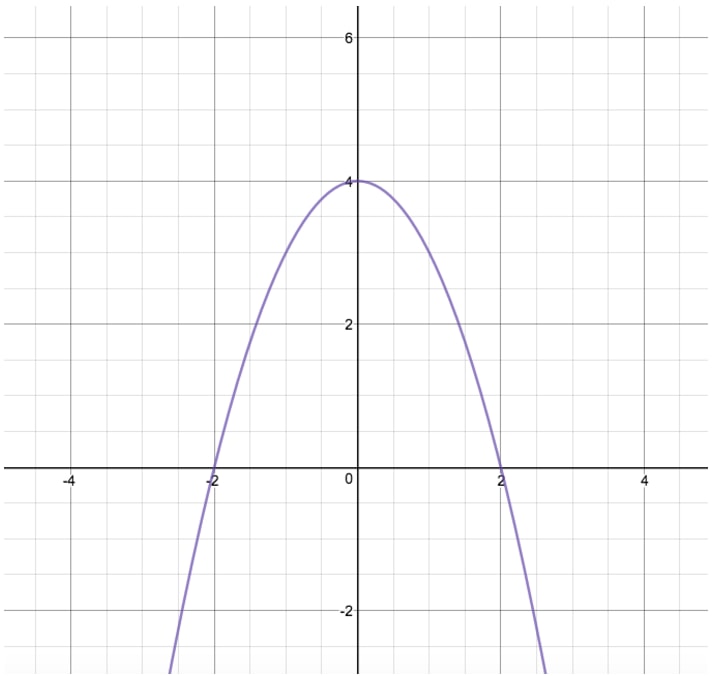



How To Reflect A Graph Through The X Axis Studypug
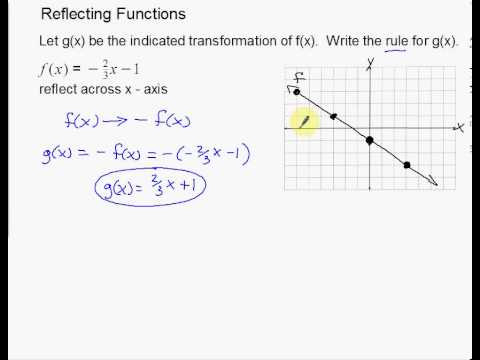



Linear Reflections Across X And Y Axis Example Youtube
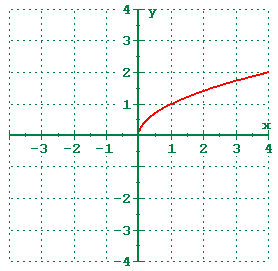



1 5 Shifting Reflecting And Stretching Graphs
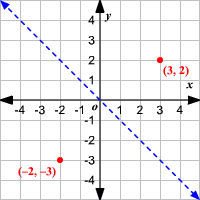



Reflections
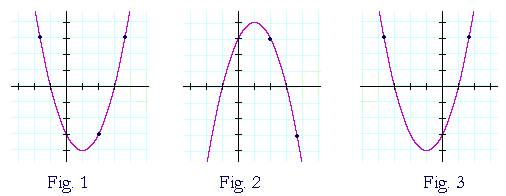



Reflections Of A Graph Topics In Precalculus
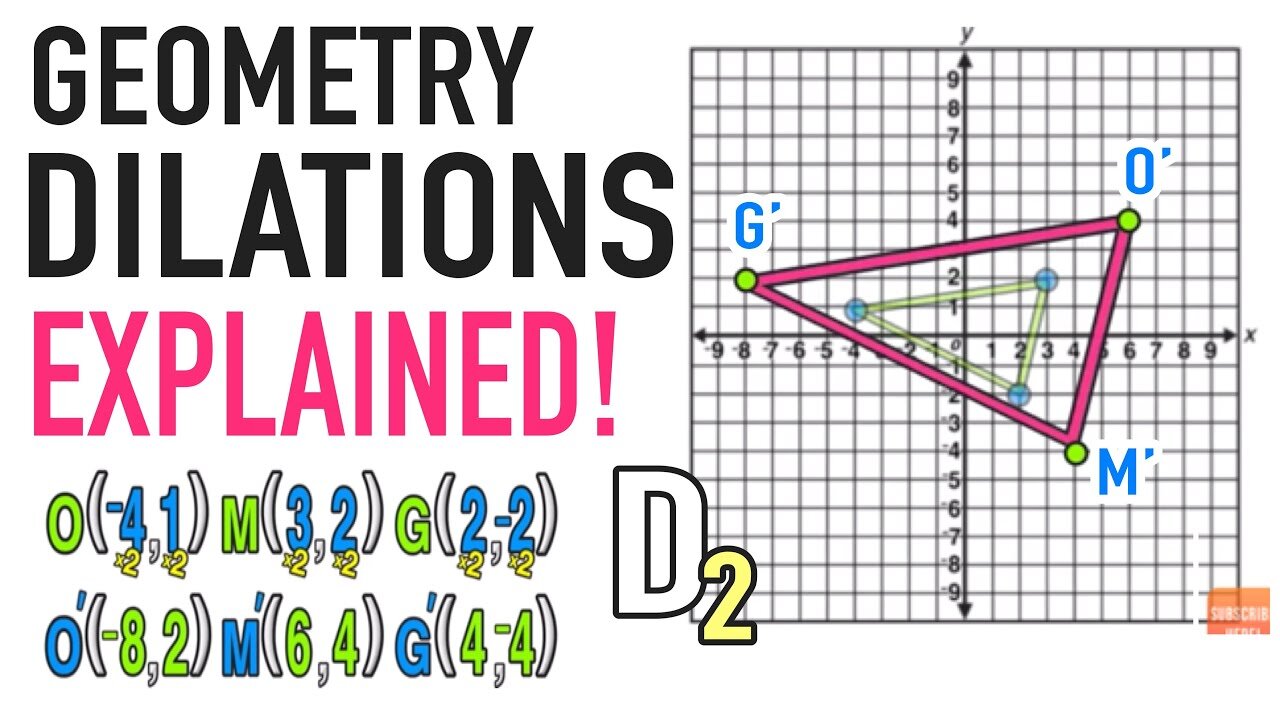



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Find The Equation Of The Graph Reflected About A Line Mathematics Stack Exchange




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
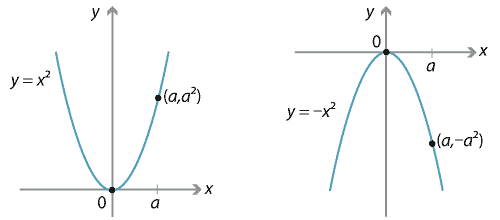



Content Transformations Of The Parabola




Inverse Function Reflection In Y Axis Mathematics Stack Exchange



1




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
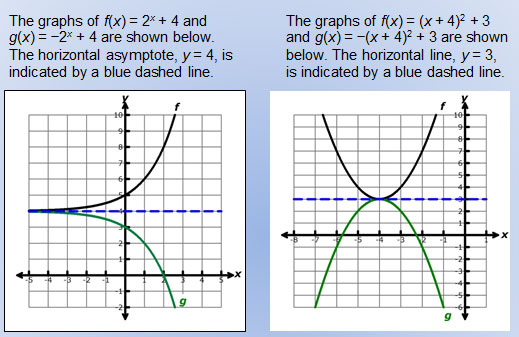



Untitled Document
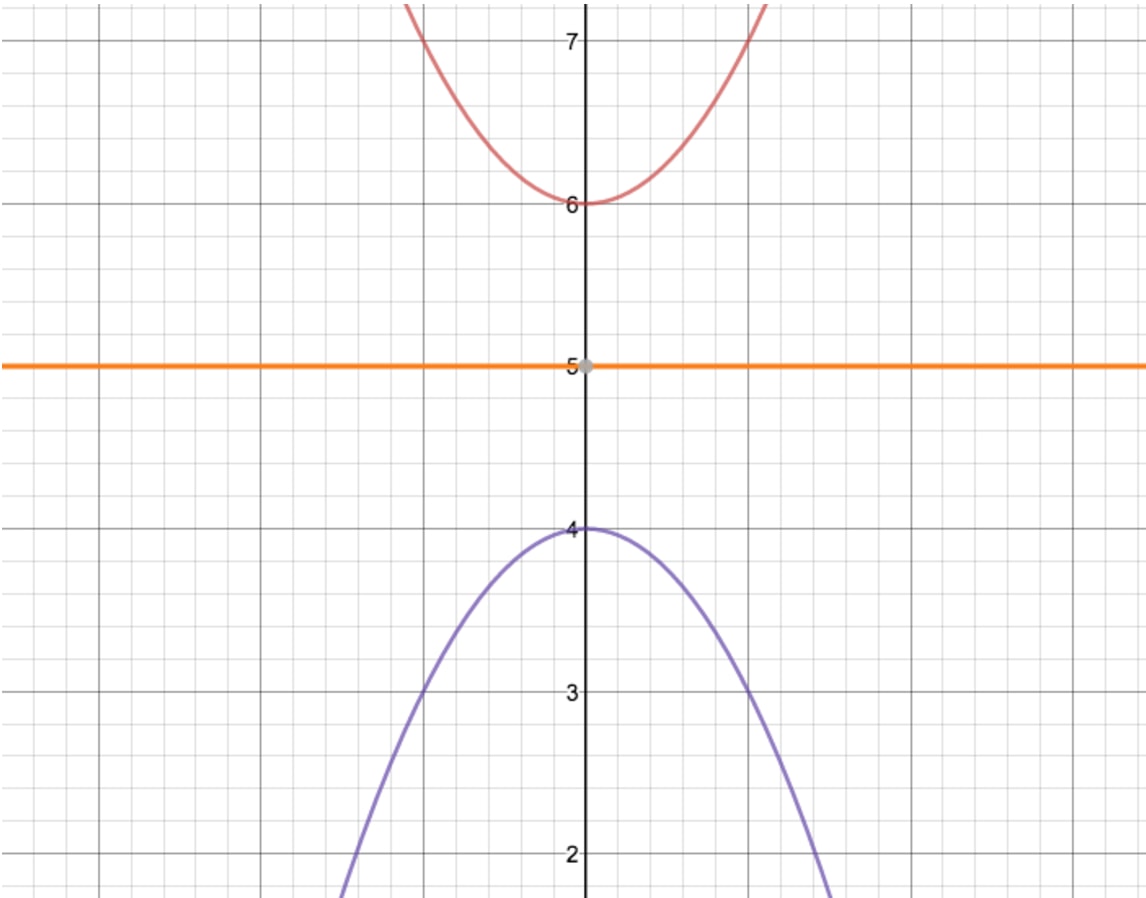



How To Reflect A Graph Through The X Axis Studypug
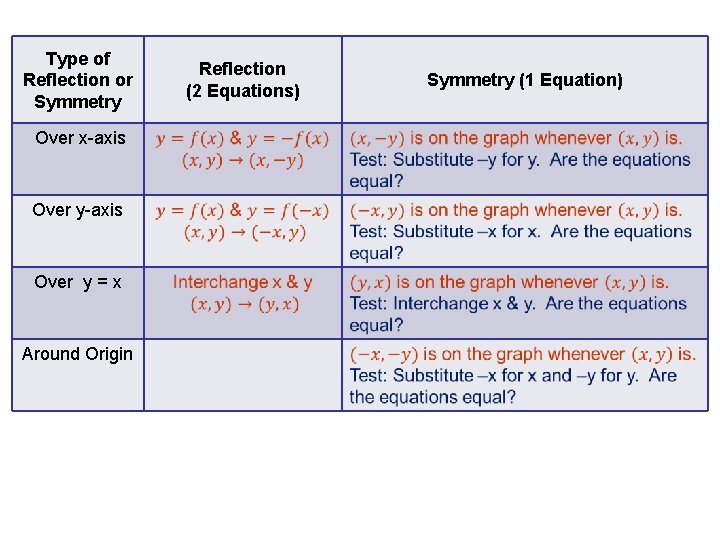



Warm Up Use The Graph To Give The



Transformations Ib Math Stuff




Reflection Transformation Matrix




Solved The Graph Shown To The Right Involves A Reflection In Chegg Com




Reflecting Functions Examples Video Khan Academy
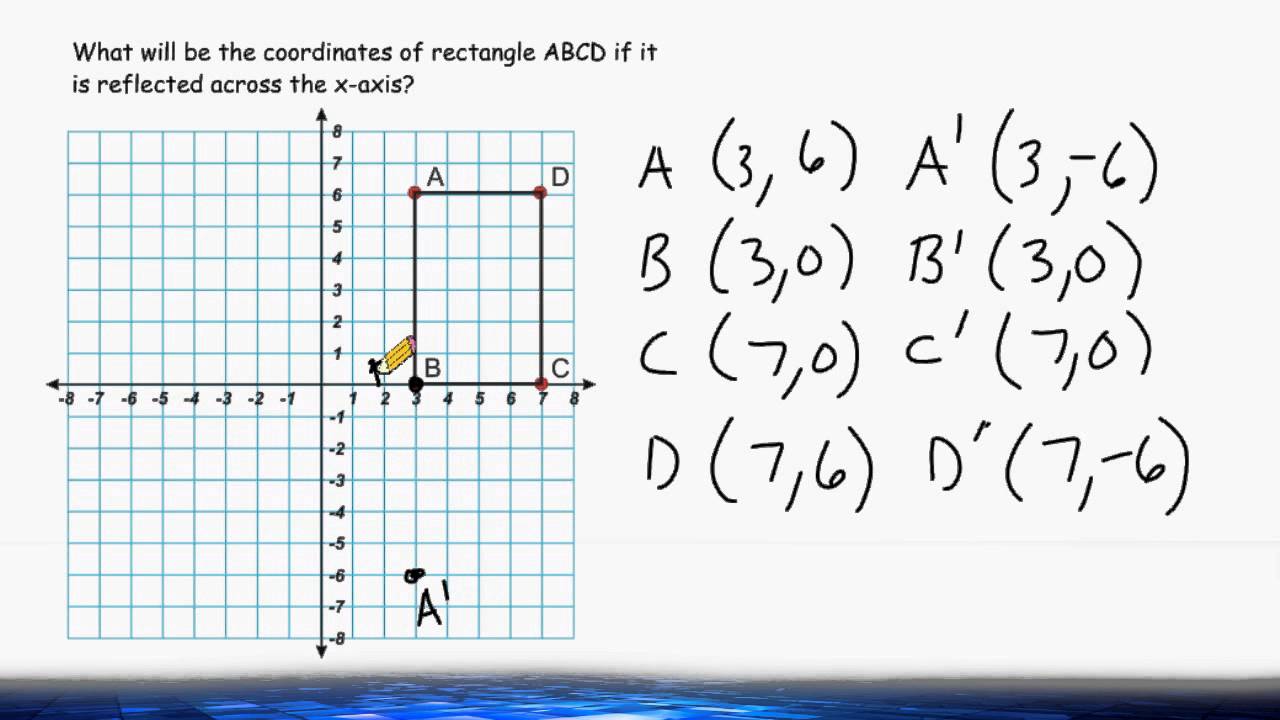



Transformations Reflection Across The X Axis Youtube



Assignment 2 Transforming Parabolas
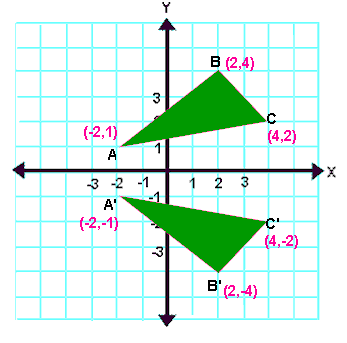



Reflection Transformation Matrix
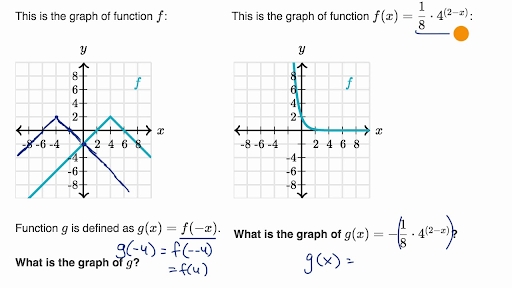



Reflecting Functions Examples Video Khan Academy



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




Common Reflections Key Stage 3



Function Transformations Reflections Across The X Axis And Y Axis Math Help From Arithmetic Through Calculus And Beyond
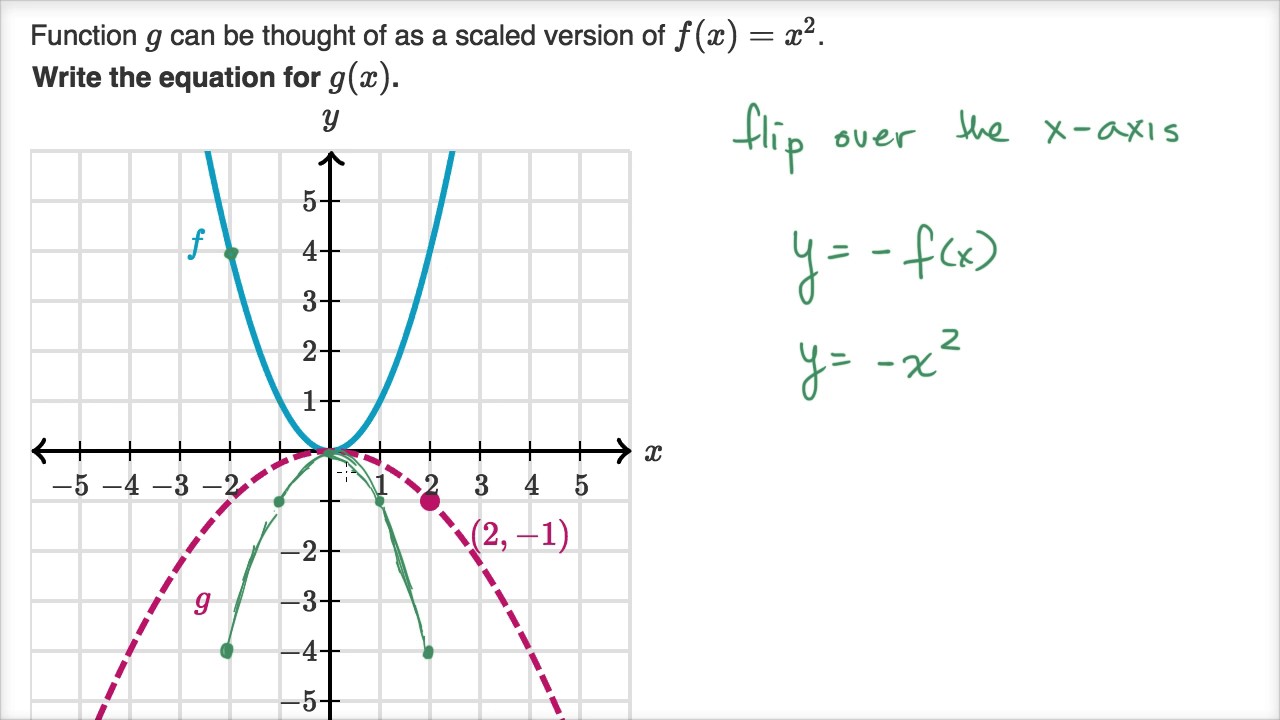



Scaling Reflecting Parabolas Video Khan Academy



Reflection Notes Videos Qa And Tests Grade 9 Optional Mathematics Transformation Kullabs
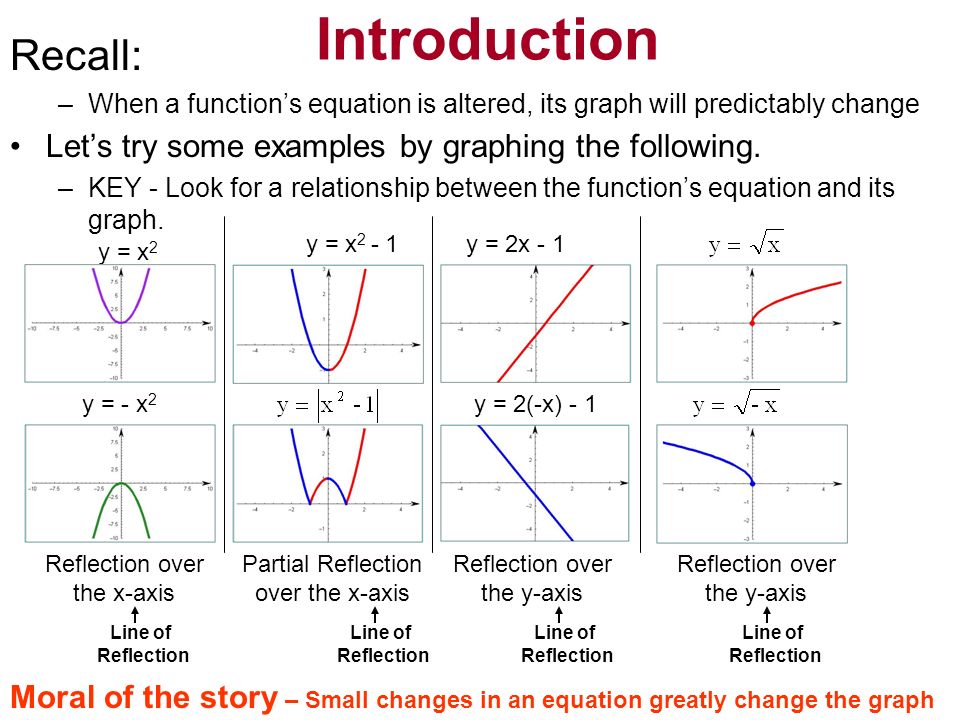



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download
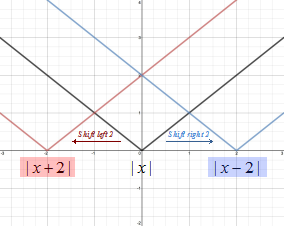



Function Transformations
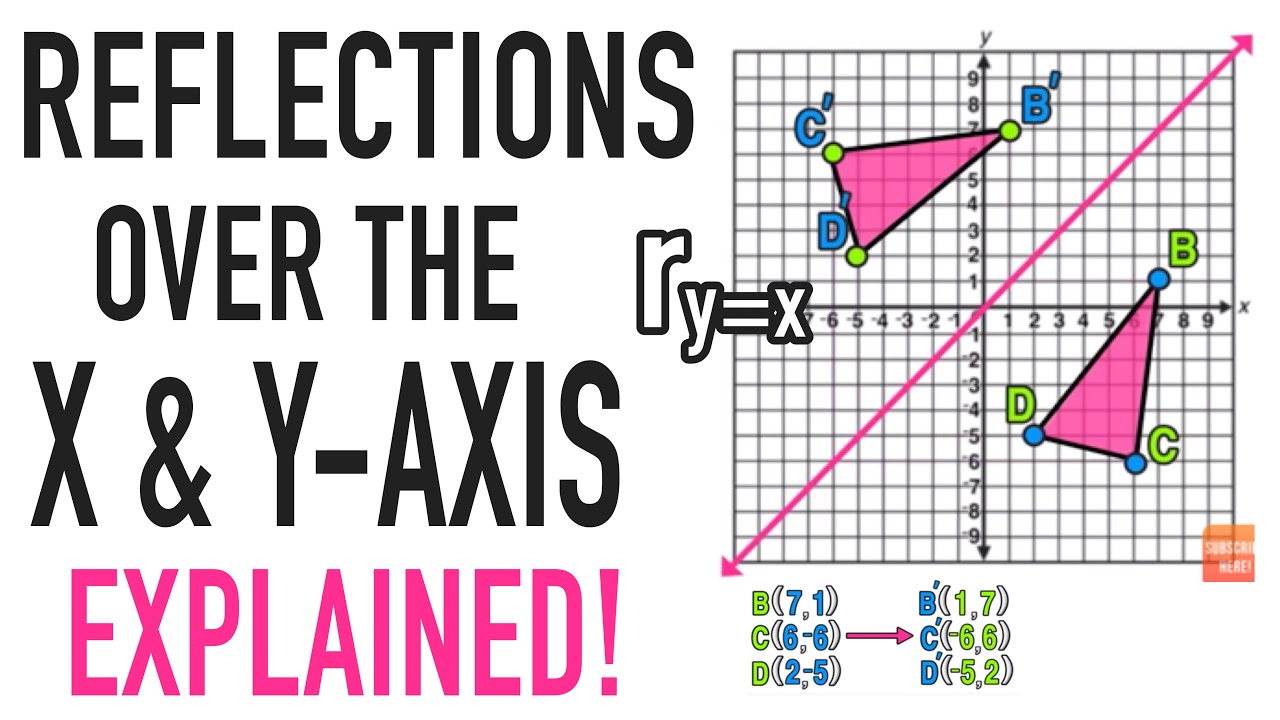



Reflections Over The X Axis And Y Axis Explained Youtube
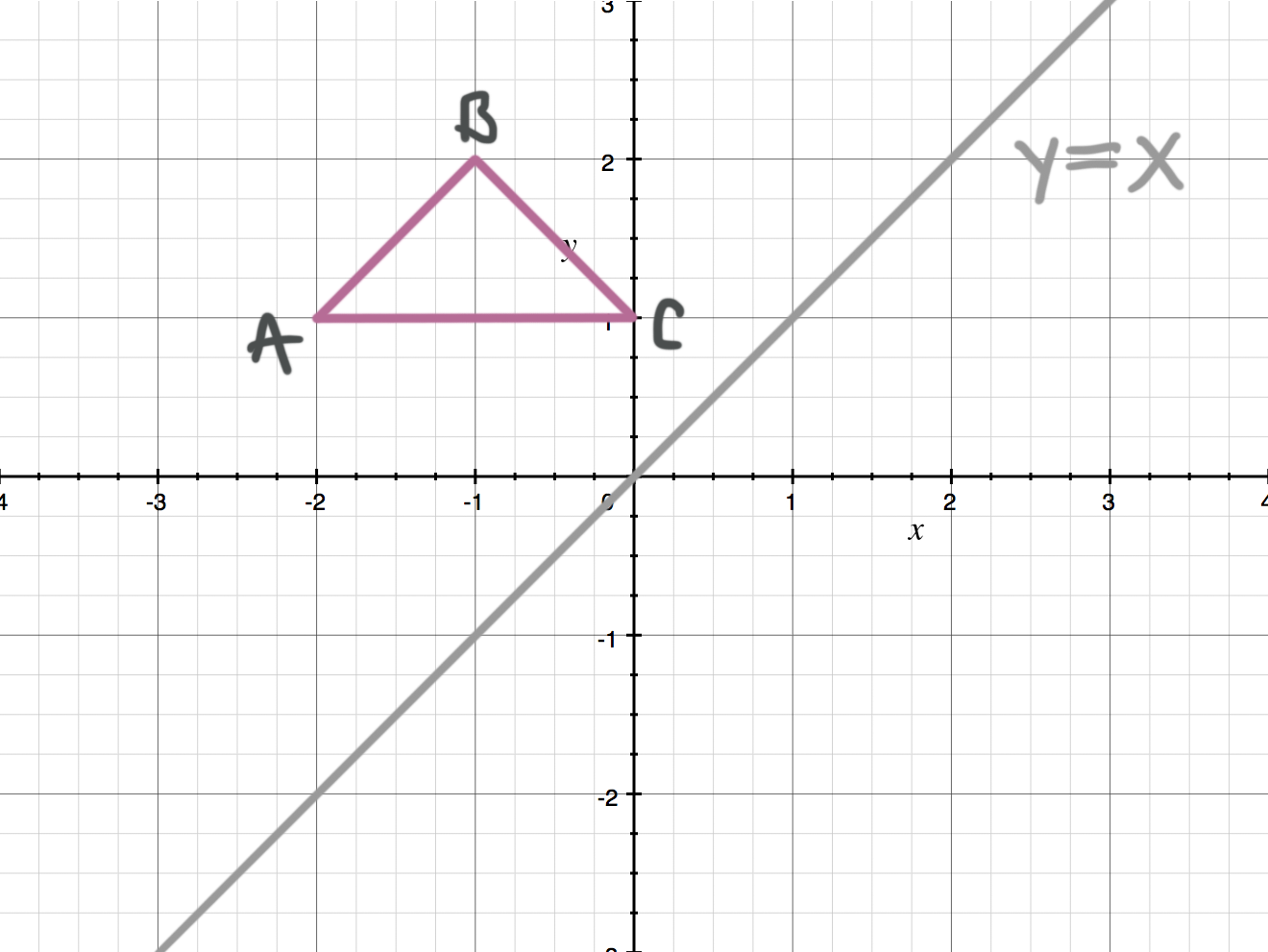



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Graphing By Translation Scaling And Reflection
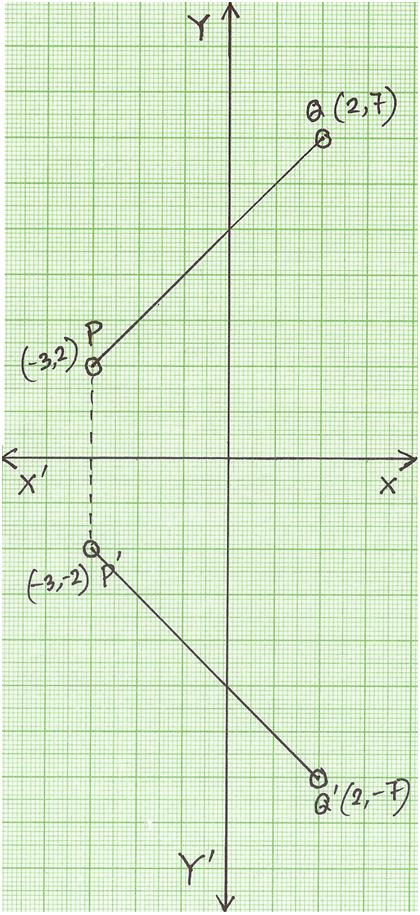



Reflection Of A Point In X Axis Reflection Of A Point Reflection




How To Reflect Quadratic Equations Video Lesson Transcript Study Com
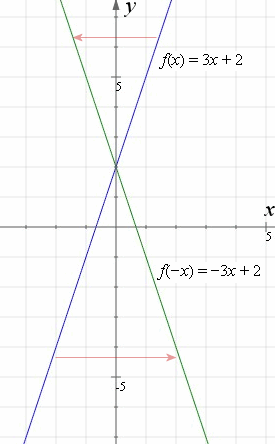



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




What Is The Equation Of This Function After It Is Reflected Over The X Axis Brainly Com



2




Transformations Reflecting Over The X Axis



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



How To Reflect A Graph Through The X Axis Studypug



Transformations Boundless Algebra




Lesson Worksheet Function Transformations Reflection Nagwa
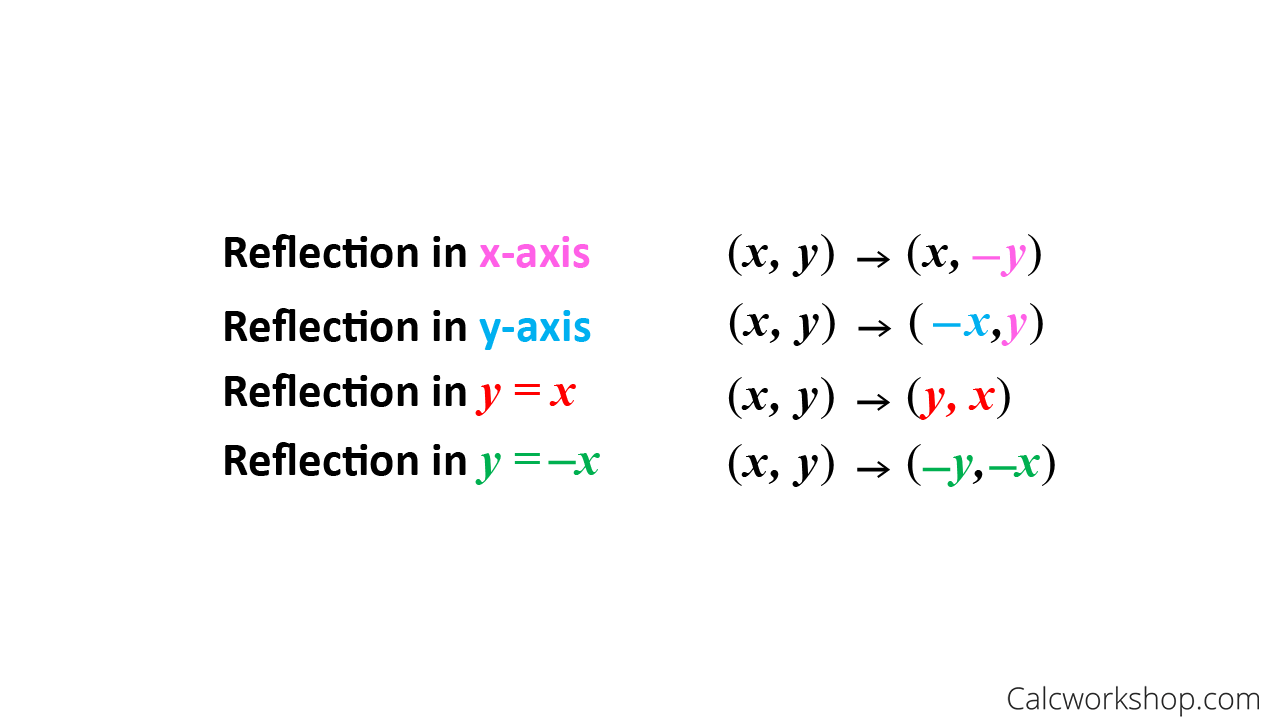



Reflection Rules How To W 25 Step By Step Examples



Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis



Reflection Objectives D Gradereflect Shapes In Lines Such As X 2 Or Y 1 Describe Reflections Fully Identify Reflection Symmetry In 3 D Solids Prior Ppt Download



A Review Of Logarithms




Using Transformations To Graph Functions



1


